Containment

[limelight]

it's a complex issue

Not at all, it's very real!

[limelight]

it's a complex issue

Not at all, it's very real!

The famous Swiss mathematician, Leonhard Euler, sort of invented the imaginary number i, and gave us the formula exp(i*a) = sin(a) + i * cos(a)
It is often quoted as exp(i*pi) + 1 = 0, but I like the more general one with any angle a.

In particular, if a = pi/2, exp( i * pi/2) = sin(pi/2) + i* cos(pi/2) = 0 + i = i

Now taking a root is the same as raising to the inverse power, for instance square root is the same as raising to power 1/2, cubic root = raising to power 1/3, so the imaginary root is the same as raising to the power 1/i

i ^ (1/i) = exp (i * pi/2)^(1/i) = exp(pi/2) = 4.81 approximately

Of course if the angle is made pi/2 +/- 2k pi , where k is any integer, the result will be the same, so 4.81 is only the first of an infinity of real numbers which, when raised to the power 1/i , yield i.

[limelight]

Maki wants me to continue with the mathematical puzzles even though she seems to be the only one participating. Are you a bit of a masochist Val? So here's one more ... but I'm beginning to run out of interesting problems.
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
A sphere, originally solid, has been drilled along one axis by a standard cylindrical drill. The remaining part measures exactly 6 cm across flats.
What is the volume of the remaining part ?

Before you ask, I tell you I did not forget to give you any data. What I gave you is enough, and the answer can be obtained rapidly by making cunning use of the lack of information. .
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

p.s. This can be handy to know for those of you who use ball valves for your through the hull isolation valves.

[mAKi]

I hope I don't have to use ball valves for valves through the hull isolation valves

[limelight]

I hope I don't have to use ball valves for valves through the hull isolation valves

Easy to say when you don't have a boat! I have two on board Limelight, one for the sink, one for the engine cooling. Ball valves are good, they open with a quarter turn, they seal very well and they are easy to maintain.

[mAKi]

so, I'll get a plumber sailor

geometric plumbing is not easy in French but in English...

[limelight]

so, I'll get a plumber sailor

geometric plumbing is not easy in French but in English...

I'll give an extra clue: I said all the information required was given, but note how I did not give the ball diameter! So maybe, if I'm right, the diameter does not matter (so long as it's more than 6 cm of course), so perhaps you can choose one that makes it easy to work out the volume.

[mAKi]

je suppose que tous les forets standard ont la même longueur donc on peut connaître le diamètre de la sphère en lui rajoutant 6 cm et faire le calcul du volume total puis en enlevant le volume du foret

[limelight]

je suppose que tous les forets standard ont la même longueur donc on peut connaître le diamètre de la sphère en lui rajoutant 6 cm et faire le calcul du volume total puis en enlevant le volume du foret

On peut remarquer que plus le diamètre de la boule diminue (tout en restant plus grand que 6 cm) plus le diamètre du foret diminue aussi pour conserver le 6 cm de hauteur de la pièce finale. A la limite, pour une sphère de diamètre 6cm, le foret devient infiniment petit et a un volume de zéro. Donc le volume de la pièce doit avoir le même volume qu'une sphère de 6cm , soit 36 π centimètres cube.

Bon ce n'est pas la preuve, c'est seulement vrai si je n'ai pas menti au départ

[limelight]

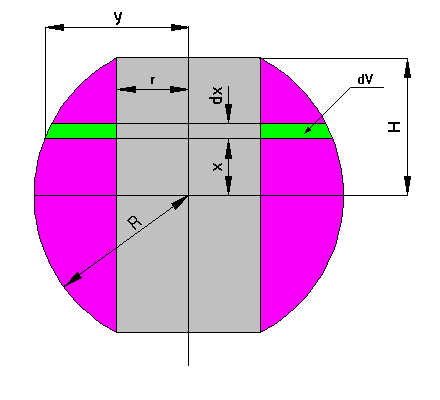
Here is a cross section of the drilled ball. The green element has a very small volume equal to:
dV = π (y^2 - r^2) * dx

Using Pythagoras' formula we see that:
r^2 = R^2 - H^2
and
y^2 = R^2 -x^2

So dV = π (H^2 - x^2) * dx

Adding all these small volumes going from x = -H to x = +H will give us the total volume, this is called integration in mathematics and it was invented by Newton in the 1600s, although I note that Archimedes, who was very precocious, used the method 2000 years earlier when he calculated the surface and volume of the sphere. But in our case, the important thing to notice is that in the formula for dV, there is no "R", only x and H appear, and x is bounded also, going from -H to +H. So that means I did not lie and the volume is independent of R. Since we calculated one particular result, the case when H = R, we therefore know that the answer is 4/3 * π * H^3 without needing to carry out the integral.

H = 3 cm
V = 36 π cubic centimetres